TEORIA DOS CONJUNTOS
Símbolos
| N: conjunto dos números naturais | |
| Z : conjunto dos números inteiros | |
| / : tal que | Q: conjunto dos números racionais |
| Q'= I: conjunto dos números irracionais | |
| R: conjunto dos números reais |
TABELA TRIGONOMÉTRICA
| Ângulo | sen | cos | tg |
| 1 | 0,017452 | 0,999848 | 0,017455 |
| 2 | 0,034899 | 0,999391 | 0,034921 |
| 3 | 0,052336 | 0,99863 | 0,052408 |
| 4 | 0,069756 | 0,997564 | 0,069927 |
| 5 | 0,087156 | 0,996195 | 0,087489 |
| 6 | 0,104528 | 0,994522 | 0,105104 |
| 7 | 0,121869 | 0,992546 | 0,122785 |
| 8 | 0,139173 | 0,990268 | 0,140541 |
| 9 | 0,156434 | 0,987688 | 0,158384 |
| 10 | 0,173648 | 0,984808 | 0,176327 |
| 11 | 0,190809 | 0,981627 | 0,19438 |
| 12 | 0,207912 | 0,978148 | 0,212557 |
| 13 | 0,224951 | 0,97437 | 0,230868 |
| 14 | 0,241922 | 0,970296 | 0,249328 |
| 15 | 0,258819 | 0,965926 | 0,267949 |
| 16 | 0,275637 | 0,961262 | 0,286745 |
| 17 | 0,292372 | 0,956305 | 0,305731 |
| 18 | 0,309017 | 0,951057 | 0,32492 |
| 19 | 0,325568 | 0,945519 | 0,344328 |
| 20 | 0,34202 | 0,939693 | 0,36397 |
| 21 | 0,358368 | 0,93358 | 0,383864 |
| 22 | 0,374607 | 0,927184 | 0,404026 |
| 23 | 0,390731 | 0,920505 | 0,424475 |
| 24 | 0,406737 | 0,913545 | 0,445229 |
| 25 | 0,422618 | 0,906308 | 0,466308 |
| 26 | 0,438371 | 0,898794 | 0,487733 |
| 27 | 0,45399 | 0,891007 | 0,509525 |
| 28 | 0,469472 | 0,882948 | 0,531709 |
| 29 | 0,48481 | 0,87462 | 0,554309 |
| 30 | 0,5 | 0,866025 | 0,57735 |
| 31 | 0,515038 | 0,857167 | 0,600861 |
| 32 | 0,529919 | 0,848048 | 0,624869 |
| 33 | 0,544639 | 0,838671 | 0,649408 |
| 34 | 0,559193 | 0,829038 | 0,674509 |
| 35 | 0,573576 | 0,819152 | 0,700208 |
| 36 | 0,587785 | 0,809017 | 0,726543 |
| 37 | 0,601815 | 0,798636 | 0,753554 |
| 38 | 0,615661 | 0,788011 | 0,781286 |
| 39 | 0,62932 | 0,777146 | 0,809784 |
| 40 | 0,642788 | 0,766044 | 0,8391 |
| 41 | 0,656059 | 0,75471 | 0,869287 |
| 42 | 0,669131 | 0,743145 | 0,900404 |
| 43 | 0,681998 | 0,731354 | 0,932515 |
| 44 | 0,694658 | 0,71934 | 0,965689 |
| 45 | 0,707107 | 0,707107 | 1 |
| 46 | 0,71934 | 0,694658 | 1,03553 |
| 47 | 0,731354 | 0,681998 | 1,072369 |
| 48 | 0,743145 | 0,669131 | 1,110613 |
| 49 | 0,75471 | 0,656059 | 1,150368 |
| 50 | 0,766044 | 0,642788 | 1,191754 |
| 51 | 0,777146 | 0,62932 | 1,234897 |
| 52 | 0,788011 | 0,615661 | 1,279942 |
| 53 | 0,798636 | 0,601815 | 1,327045 |
| 54 | 0,809017 | 0,587785 | 1,376382 |
| 55 | 0,819152 | 0,573576 | 1,428148 |
| 56 | 0,829038 | 0,559193 | 1,482561 |
| 57 | 0,838671 | 0,544639 | 1,539865 |
| 58 | 0,848048 | 0,529919 | 1,600335 |
| 59 | 0,857167 | 0,515038 | 1,664279 |
| 60 | 0,866025 | 0,5 | 1,732051 |
| 61 | 0,87462 | 0,48481 | 1,804048 |
| 62 | 0,882948 | 0,469472 | 1,880726 |
| 63 | 0,891007 | 0,45399 | 1,962611 |
| 64 | 0,898794 | 0,438371 | 2,050304 |
| 65 | 0,906308 | 0,422618 | 2,144507 |
| 66 | 0,913545 | 0,406737 | 2,246037 |
| 67 | 0,920505 | 0,390731 | 2,355852 |
| 68 | 0,927184 | 0,374607 | 2,475087 |
| 69 | 0,93358 | 0,358368 | 2,605089 |
| 70 | 0,939693 | 0,34202 | 2,747477 |
| 71 | 0,945519 | 0,325568 | 2,904211 |
| 72 | 0,951057 | 0,309017 | 3,077684 |
| 73 | 0,956305 | 0,292372 | 3,270853 |
| 74 | 0,961262 | 0,275637 | 3,487414 |
| 75 | 0,965926 | 0,258819 | 3,732051 |
| 76 | 0,970296 | 0,241922 | 4,010781 |
| 77 | 0,97437 | 0,224951 | 4,331476 |
| 78 | 0,978148 | 0,207912 | 4,70463 |
| 79 | 0,981627 | 0,190809 | 5,144554 |
| 80 | 0,984808 | 0,173648 | 5,671282 |
| 81 | 0,987688 | 0,156434 | 6,313752 |
| 82 | 0,990268 | 0,139173 | 7,11537 |
| 83 | 0,992546 | 0,121869 | 8,144346 |
| 84 | 0,994522 | 0,104528 | 9,514364 |
| 85 | 0,996195 | 0,087156 | 11,43005 |
| 86 | 0,997564 | 0,069756 | 14,30067 |
| 87 | 0,99863 | 0,052336 | 19,08114 |
| 88 | 0,999391 | 0,034899 | 28,63625 |
| 89 | 0,999848 | 0,017452 | 57,28996 |
| 90 | 1 | 0 | - |
Vetores
Reta Orientada - Eixo
Uma reta r é orientada quando fixa nela um sentido de percurso, considerado positivo e indicado por uma seta.

Segmento orientado
Um segmento orientado é determinado por um par ordenado de pontos, o primeiro chamado origem do segmento, o segundo chamado extremidade.

Segmento Nulo
Um segmento nulo é aquele cuja extremidade coincide com a origem.
Segmentos Opostos
Se AB é um segmento orientado, o segmento orientado BA é oposto de AB.
Medida de um Segmento
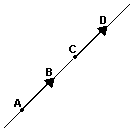
Fixada uma unidade de comprimento, cada segmento orientado pode-se associar um número real, não negativo, que é a medida do segmento em relação aquela unidade. A medida do segmento orientado é o seu comprimento ou seu módulo. O comprimento do segmento AB é indicado por 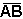 .
.
Assim, o comprimento do segmento AB representado na figura abaixo é de 5 unidades de comprimento:
Observações
- Os segmentos nulos têm comprimento igual a zero
-
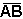 =
= 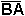 .
.
Direção e Sentido
Dois segmentos orientados não nulos AB e CD têm a mesma direção se as retas suportes desses segmentos são paralelas:
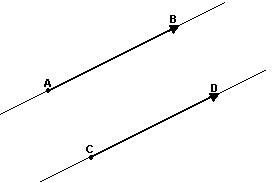
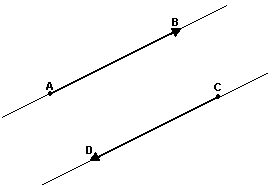
ou coincidentes
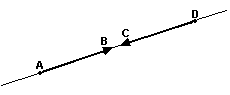 |  |
Observações
- Só se pode comparar os sentidos de dois segmentos orientados se eles têm mesma direção.
- Dois Segmentos orientados opostos têm sentidos contrários.
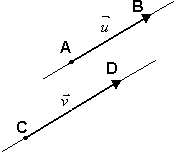
Segmentos Equipolentes
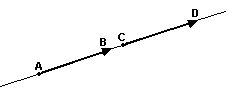
Dois segmentos orientados AB e CD são equipolentes quando têm a mesma direção, o mesmo sentido e o mesmo comprimento.
Se os segmentos orientados AB e CD não pertencem à mesma reta. Na segunda figura abaixo, para que AB seja equipolente a CD é necessário que AB//CD e AC/BD, isto é, ABCD deve ser um paralelogramo.
 | 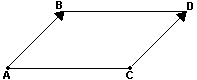 |
Observações
- Dois segmentos nulos são sempre equipolentes.
- A equipolência dos segmentos AB e CD é representada por AB ~ CD.
Propriedades da Equipolência
- AB ~ AB (reflexiva).
- Se AB ~ CD, CD ~ AB (simétrica).
- Se AB ~ CD e CD ~ EF, AB ~ EF (transitiva).
- Dado o segmento orientado AB e um ponto C, existe um único ponto D tal que AB ~ CD.
Vetor
Vetor determinado por um segmento orientado AB é o conjunto de todos os segmentos orientados equipolentes a AB.
Se indicarmos com  este conjunto, simbolicamente poderemos escrever:
este conjunto, simbolicamente poderemos escrever:
onde XY é um segmento qualquer do conjunto.
O vetor determinado por AB é indicado por 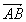 ou B - A ou
ou B - A ou  .
.
um mesmo vetor 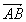 é determinado por uma infinidade de segmentos orientados, chamados representantes desse vetor, e todos equipolentes entre si. Assim, um segmento determina um conjunto que é o vetor, e qualquer um destes representantes determina o mesmo vetor. Usando um pouco mais nossa capacidade de abstração, se considerarmos todos os infinitos segmentos orientados de origem comum, estaremos caracterizando, através de representantes, a totalidade dos vetores do espaço. Ora, cada um destes segmentos é um representante de um só vetor. Conseqüentemente, todos os vetores se acham representados naquele conjunto que imaginamos.
é determinado por uma infinidade de segmentos orientados, chamados representantes desse vetor, e todos equipolentes entre si. Assim, um segmento determina um conjunto que é o vetor, e qualquer um destes representantes determina o mesmo vetor. Usando um pouco mais nossa capacidade de abstração, se considerarmos todos os infinitos segmentos orientados de origem comum, estaremos caracterizando, através de representantes, a totalidade dos vetores do espaço. Ora, cada um destes segmentos é um representante de um só vetor. Conseqüentemente, todos os vetores se acham representados naquele conjunto que imaginamos.
As características de um vetor  são as mesmas de qualquer um de seus representantes, isto é: o módulo, a direção e o sentido do vetor são o módulo, direção e o sentido de qualquer um de seus representantes.
são as mesmas de qualquer um de seus representantes, isto é: o módulo, a direção e o sentido do vetor são o módulo, direção e o sentido de qualquer um de seus representantes.
O módulo de  se indica por |
se indica por | | .
| .
Vetores iguais
Dois vetores 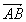 e
e 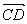 são iguais se, e somente se, AB ~ CD.
são iguais se, e somente se, AB ~ CD.
Vetor Nulo
Os segmentos nulos, por serem equipolentes entre si, determinam um único vetor, chamado vetor nulo ou vetor zero, e que é indicado por 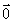 .
.
Vetores Opostos
Dado um vetor  =
= 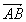 , o vetor
, o vetor 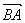 é o oposto de
é o oposto de 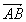 e se indica por
e se indica por 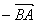 ou por
ou por 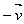 .
.
Vetor Unitário
Um vetor  é unitário se |
é unitário se | | = 1.
| = 1.
Versor
Versor de um vetor não nulo  é o vetor unitário de mesma direção e mesmo sentido de
é o vetor unitário de mesma direção e mesmo sentido de  .
.
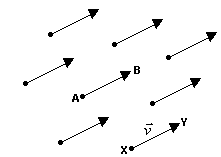
Por exemplo, tomemos um vetor  de módulo 3.
de módulo 3.
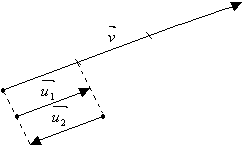
Os vetores  e
e 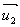 da figura são vetores unitários, pois ambos têm módulo 1. No entanto, apenas
da figura são vetores unitários, pois ambos têm módulo 1. No entanto, apenas  tem a mesma direção e o mesmo sentido de
tem a mesma direção e o mesmo sentido de  . Portanto, este é o versor de
. Portanto, este é o versor de  .
.
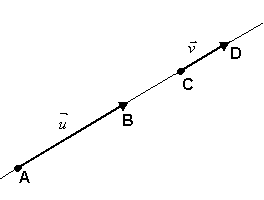
Vetores Colineares
Dois vetores 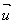 e
e  são colineares se tiverem a mesma direção. Em outras palavras:
são colineares se tiverem a mesma direção. Em outras palavras: 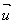 e
e  são colineares se tiverem representantes AB e CD pertencentes a uma mesma reta ou a retas paralelas.
são colineares se tiverem representantes AB e CD pertencentes a uma mesma reta ou a retas paralelas.
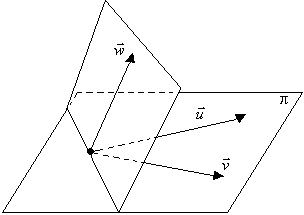
Vetores Coplanares
Se os vetores não nulos 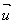 ,
,  e
e 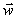 (não importa o número de vetores) possuem representantes AB, CD e EF pertencentes a um mesmo plano p, diz-se que eles são coplanares.
(não importa o número de vetores) possuem representantes AB, CD e EF pertencentes a um mesmo plano p, diz-se que eles são coplanares.
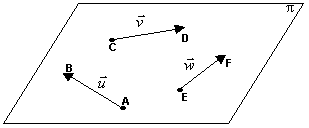
Dois vetores  e
e  quaisquer são são sempre coplanares, pois podemos sempre tomar um ponto no espaço e, com origem nele, imaginar os dois representantes de
quaisquer são são sempre coplanares, pois podemos sempre tomar um ponto no espaço e, com origem nele, imaginar os dois representantes de  e
e  pertencendo a um plano p que passa por este ponto.
pertencendo a um plano p que passa por este ponto.
Três vetores poderão ou não ser coplanares.
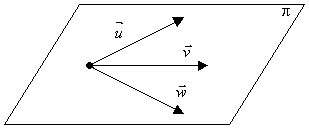
Soma de vetores
Se v=(a,b) e w=(c,d), definimos a soma de v e w, por:
v + w = (a+c,b+d)
Propriedades da soma de vetores
| I) Comutativa: Para todos os vetores u e v de R2: v + w = w + v II) Associativa: Para todos os vetores u, v e w de R2: u + (v + w) = (u + v) + w III) Elemento neutro: Existe um vetor O=(0,0) em R2 tal que para todo vetor u de R2, se tem: O + u = u IV) Elemento oposto: Para cada vetor v de R2, existe um vetor -v em R2 tal que: v + (-v) = O |
Diferença de vetores
Se v=(a,b) e w=(c,d), definimos a diferença entre v e w, por:
v - w = (a-c,b-d)
Produto de um escalar por um vetor
Se v=(a,b) é um vetor e c é um número real, definimos a multiplicação de c por v, como:
c.v = (ca,cb)
Propriedades do produto de escalar por vetor
Quaisquer que sejam k e c escalares, v e w vetores:
|
Módulo de um vetor
O módulo ou comprimento do vetor v=(a,b) é um número real não negativo, definido por:
Vetor unitário
Vetor unitário é o que tem o módulo igual a 1.
Existem dois vetores unitários que formam a base canônica para o espaço R2, que são dados por:
i = (1,0) j = (0,1)
Para construir um vetor unitário u que tenha a mesma direção e sentido que um outro vetor v, basta dividir o vetor v pelo seu módulo, isto é:
Observação:
Para construir um vetor u paralelo a um vetor v, basta tomar u=cv onde c é um escalar não nulo. Nesse caso, u e v serão paralelos.
Se c = 0 então u será o vetor nulo.
Se 0 < c < 1 então u terá comprimento menor do que v.
Se c > 1 então u terá comprimento maior do que v.
Se c < 0 então u terá sentido oposto ao de v.
Se 0 < c < 1 então u terá comprimento menor do que v.
Se c > 1 então u terá comprimento maior do que v.
Se c < 0 então u terá sentido oposto ao de v.
Produto escalar
Dados os vetores u=(a,b) e v=(c,d), definimos o produto escalar entre os vetores u e v, como o número real obtido por:
u.v = a.c + b.d
Exemplos:
O produto escalar entre u=(3,4) e v=(-2,5) é:
u.v = 3.(-2) + 4.(5) = -6+20 = 14
O produto escalar entre u=(1,7) e v=(2,-3) é:
u.v = 1.(2) + 7.(-3) = 2-21 = -19
Propriedades do produto escalar
Quaisquer que sejam os vetores, u v e w e k escalar:
| v.w = w.v v.v = |v| |v| = |v|2 u.(v+w) = u.v + u.w (kv).w = v.(kw) = k(v.w) |kv| = |k| |v| |u.v| <= |u| |v| (desigualdade de Schwarz) |u+v| <= |u| + |v| (desigualdade triangular) Obs: <= significa menor ou igual |
Ângulo entre dois vetores
O produto escalar entre os vetores u e v pode ser escrito na forma:
u.v = |u| |v| cos(x)
onde x é o ângulo formado entre u e v.
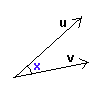
Através desta última definição de produto escalar, podemos obter o ângulo x entre dois vetores genéricos u e v, como:
desde que nenhum deles seja nulo.
Vetores ortogonais
Dois vetores u e v são ortogonais se:
u.v = 0
Fonte: Só Matemática
Muito grato pela visita, bons estudos e boa sorte!
Deixe seus comentários.
Fique com Deus,
Seja bem-vindo(a) e volte sempre...


1 comentários:
nossa isso é grande mesmo...
mais acho que é um bom conteudo para trabalhos sobre o assunto..
os alunos se interessaram bastante..
Postar um comentário